






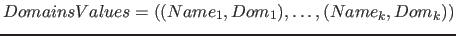
There are two types of domain information:
 : Domains for possible values (including values of variables) an element can contain.
: Domains for possible values (including values of variables) an element can contain.
 : Domains for used values in elements.
: Domains for used values in elements.
The specification of a domain consists of two parts  and
and 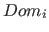 .
.
The first part of the domain entry is the name 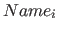 of the element, for which the domain is. Elements/names that can be set for the domains are listed in table 5 on page
of the element, for which the domain is. Elements/names that can be set for the domains are listed in table 5 on page ![[*]](../pictures/crossref.png) .
.
Also listed there are the standard domains of the elements.
Of the listed standard domains the scalar (sub-)domains can be changed, the number of scalar subdomains of a domain, however, should not be changed (if not specified otherwise). So if the standard domain of an element is for scalars values (e. g. 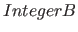 ), for this element never a vector domain should be set. On the other hand, if the standard domain of an element is for vectors with
), for this element never a vector domain should be set. On the other hand, if the standard domain of an element is for vectors with 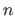 elements, for this element only domains should be set, which are for vectors with
elements, for this element only domains should be set, which are for vectors with 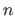 elements. In this way, for example, properties can be always interpreted in the same way.
For elements (e. g. Properties), which are not listed in table 5, the domains can of course be set freely.
elements. In this way, for example, properties can be always interpreted in the same way.
For elements (e. g. Properties), which are not listed in table 5, the domains can of course be set freely.
The second part of the domain entry is the domain 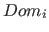 to apply to the element
to apply to the element 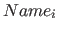 . A list of the possible domains is given in table 6 on page
. A list of the possible domains is given in table 6 on page ![[*]](../pictures/crossref.png) .
.
Values outside of their domain are rounded to values in the domain. The rounded value of a (scalar) number, is the value with the minimum distance to the not rounded value. If there are several of them, the smallest value of them is taken, as the rounded value.
Rounding of vectors is done with their distance. The distance between two vectors is the sum of the distances of their elements. The rounded vector of a domain is the vector in the domain with the smallest distance from the unrounded vector. If several vectors have a minimum distance from the unrounded vector, the rounded vector is the vector, whose first 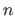 elements have a minimal distance from the unrounded vector. Where
elements have a minimal distance from the unrounded vector. Where 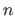 , starting from the number of elements in the unrounded vector, is reduced by one till a vector is found or 1 is reached. If even then more vectors remain, the rounded vector is the vector, whose
, starting from the number of elements in the unrounded vector, is reduced by one till a vector is found or 1 is reached. If even then more vectors remain, the rounded vector is the vector, whose 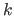 'th element is less than the
'th element is less than the 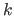 'th element of the other remaining vectors, where
'th element of the other remaining vectors, where 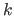 is counted from 1 to the number of elements in the vector.
is counted from 1 to the number of elements in the vector.
If the vector to be rounded has too many elements, the number of its elements is reduced to the correct number. Should the to round vector contain not enough elements, the missing elements are created and assigned to the zero value of the respective element domains.
Each domain has a null value. The null value of a scalar domain (a domain for numbers), is the value 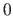 rounded to a value in the domain.
For vectors the null vector is the vector, which is generated if a vector whose elements are all
rounded to a value in the domain.
For vectors the null vector is the vector, which is generated if a vector whose elements are all 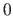 is rounded to a vector in the domain.
is rounded to a vector in the domain.
Each scalar domain has a maximum value and minimum value. The maximum value is the highest value in the domain and the minimum value is the smallest value.
The domains, which contain only integers, have a scale factor  , which apply for the corresponding element of the
, which apply for the corresponding element of the 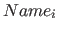 . This factor
. This factor  is a floating point number, with which the values of the unscaled domain are multiplied, to obtain the scaled domain. As standard, the scaling factor
is a floating point number, with which the values of the unscaled domain are multiplied, to obtain the scaled domain. As standard, the scaling factor 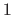 is assumed. The scaling factor is useful for example, if the horizontal dimension should not be measured in meter
is assumed. The scaling factor is useful for example, if the horizontal dimension should not be measured in meter 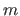 but in milli meter
but in milli meter 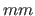 or when the temperature is not given in degrees Kelvin, but in tenth of a degree Kelvin.
or when the temperature is not given in degrees Kelvin, but in tenth of a degree Kelvin.
In the following notation the scale factor is indicated by the notation, that the domain is multiplied with it "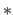 ". A Skalierungsfaltor of
". A Skalierungsfaltor of 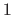 is not specified here. For example, "
is not specified here. For example, "
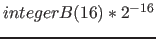 " means that the 16-bit integer domain is scaled with the scaling factor
" means that the 16-bit integer domain is scaled with the scaling factor 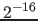 . In contrast "
. In contrast "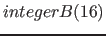 " means that the scaling factor is
" means that the scaling factor is 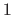 , that is the domain is not scaled.
, that is the domain is not scaled.
Example: The basis domain is for integers from 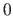 to
to 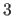 (which are 4 values) with the scaling factor
(which are 4 values) with the scaling factor 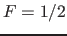 . Possible values are:
. Possible values are: 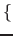
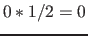 ;
; 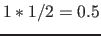 ;
; 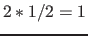 ;
; 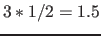
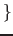 . If a number in an element for the domain is for example unscaled
. If a number in an element for the domain is for example unscaled 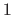 , it is interpreted as the scaled number
, it is interpreted as the scaled number 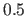 .
.
| Name | Description | Standard domain |
dim( 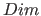 , , 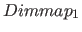 , ,  , , 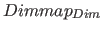 ) ) |
This is the domain for position vectors. The number 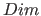 is the number of dimensions respectively elements of a position vector. The value is the number of dimensions respectively elements of a position vector. The value 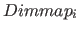 is an integer, which determines, in which direction the dimension is an integer, which determines, in which direction the dimension 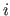 will be mapped (see table 7 on page will be mapped (see table 7 on page ![[*]](../pictures/crossref.png) for the possible values, there numerical values are specified [in the "value" column]). The domain is a vector with for the possible values, there numerical values are specified [in the "value" column]). The domain is a vector with 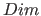 numbers (or scalars). The default value for the number of dimensions numbers (or scalars). The default value for the number of dimensions 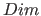 is is 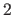 , it will be used, if no domain is specified for position vectors. Then (standard case) the first dimension points in the horizontally direction and the second dimension in the vertically direction. Regardless of this, the direction value , it will be used, if no domain is specified for position vectors. Then (standard case) the first dimension points in the horizontally direction and the second dimension in the vertically direction. Regardless of this, the direction value 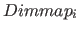 of the domains for elements of the domains for elements  (also inherited) overrides the value domains (also inherited) overrides the value domains  . Normally, however, the direction specifications should be the same for all position vector domains. . Normally, however, the direction specifications should be the same for all position vector domains. |
 , , 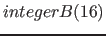 , ,
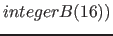 |
| subfunction | values which can appear in subfunctions | 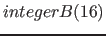 |
| area | domain for the area element (see section 9.6 on page ![[*]](../pictures/crossref.png) ) ) |
  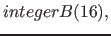
 |
| inVar(i) | domain for the i'th input variable (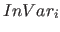 ) ) |
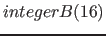 |
| set | zeroth domain for set-elements |



 |
| set(i) | i'th domain for set-elements |



 |
| matrix | zeroth domain for matrix elements |



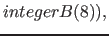

 |
| matrix(i) | i'th domain for matrix elements |



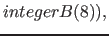

 |
| externSubobject( Number ) | The domain for the external subobject with the given number (see section 9.10 on page ![[*]](../pictures/crossref.png) ) of the multimedia object. The output values of the external subobject with the given number can be set to the values of this domain. In the main-Fib-object ) of the multimedia object. The output values of the external subobject with the given number can be set to the values of this domain. In the main-Fib-object  for each externSubobjectOutput domain external subobjects with the given number can exist. Also for each external subobject (each number) in the main-Fib-object for each externSubobjectOutput domain external subobjects with the given number can exist. Also for each external subobject (each number) in the main-Fib-object  an externSubobjectOutput domain with the number should exist. At least for the external subobjects with the highest number an externSubobject domain have to be created, so that it is known, how much external subobjects in the main-Fib-object an externSubobjectOutput domain with the number should exist. At least for the external subobjects with the highest number an externSubobject domain have to be created, so that it is known, how much external subobjects in the main-Fib-object  exists. The externSubobjectOutput domain isn't inherited by other root-elements. exists. The externSubobjectOutput domain isn't inherited by other root-elements. |
 |
| property( Name ) | domain of the properties for the given  ; see table 2 on page ; see table 2 on page ![[*]](../pictures/crossref.png) for the possible names ( for the possible names ( ) ) |
dependent of the type ( ) of the property ) of the property |
| property( whatever ) | The properties of the points dosn't matter. Whatever properties are assigned to a point with this property, they are correct. |  |
| property( colorRGB) | domain for RGB-colors | 
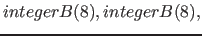 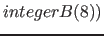 |
| property( colorGrayscale ) | domain for monocrome colors |  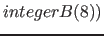 |
| property( layer ) | number of possible layers |  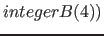 |
| property( transparency ) | transparency of the points |  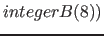 |
| property( persistent ) | This property is only useful for a period of time. Points in space with this property only lose their other properties, if they are overwritten by a respective property of the same type. This of however is only the case, as long as the particular point has the property 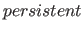 . This property is for example useful, if in a movie objects should be visible as long as they are not overwritten by other objects. In this case, the entire background can get the property . This property is for example useful, if in a movie objects should be visible as long as they are not overwritten by other objects. In this case, the entire background can get the property  . If an object is defined and displayed at a time, it will be there in the future as long as it won't get overwritten. (The possible values are . If an object is defined and displayed at a time, it will be there in the future as long as it won't get overwritten. (The possible values are 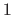 for persistent and for persistent and 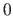 for non persistent.) for non persistent.) |
 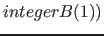 |
| property( sound ) | a sound; the values are: 1. frequency in Hertz (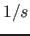 ), 2. sound pressure in Pascal ), 2. sound pressure in Pascal 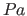 ( (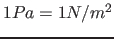 ), 3. phase shift in radians, 4. duration in seconds; a sound is additive to other sounds ), 3. phase shift in radians, 4. duration in seconds; a sound is additive to other sounds |
 , , 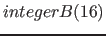 , , 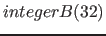 , ,
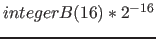 , ,
 |
| property( soundPolarized ) | a sound; the values are: 1. frequency in Hertz (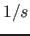 ), 2. sound pressure in Pascal ), 2. sound pressure in Pascal 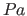 ( (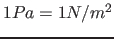 ), 3. phase shift in radians, 4. duration in seconds; r = ), 3. phase shift in radians, 4. duration in seconds; r =  to ( to (
 ) polarization fraction (as an angle in radians) in the dimension plane, which is spanned by the respective dimensions ) polarization fraction (as an angle in radians) in the dimension plane, which is spanned by the respective dimensions  and and 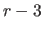 ( ( is the number of dimensions), the angle origin is the is the number of dimensions), the angle origin is the 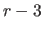 axis and goes in positive direction; a sound is additive to other sounds axis and goes in positive direction; a sound is additive to other sounds |
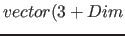 , , 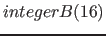 , , 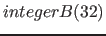 , ,
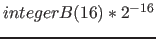 , ,
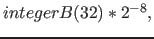
![$[integerB(16) * 2^{-16}]^{Dim-1} )$](img394.png) |
| property( soundAmplitude ) | the amplitude of a sound; the values are: 1. sound pressure in Pascal 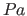 ( (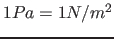 ), 2. phase shift in radians, 3. duration in seconds; a sound is additive to other sounds; With this properties sounds can be build by their amplitude with a specific sampling rate, such as in the WAVE file format. ), 2. phase shift in radians, 3. duration in seconds; a sound is additive to other sounds; With this properties sounds can be build by their amplitude with a specific sampling rate, such as in the WAVE file format. |
 , ,
 , ,
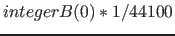 , ,
 |
| property( soundBarrier ) | speed of sound in meters per second ( ); With this property objects can change the acoustics. ); With this property objects can change the acoustics. |
 , ,
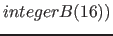 |
| property( soundReflected ) | fraction of sound reflected from the object; This property applies to the surface/the edge of the object and not for all his individual points |  , ,
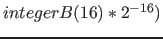 |
| property( soundDamping ) | fraction of the sound swallowed by a point |  , ,
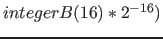 |
| property( kelvin ) | temperature in Kelvin |  , ,
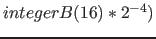 |
| property( electroMagnetic ) | an electromagnetic radiation source, the values are: 1. frequency in Hertz (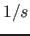 ), 2. amplitude in Candela cd, 3. phase shift in radians, 4. duration in seconds, r = ), 2. amplitude in Candela cd, 3. phase shift in radians, 4. duration in seconds, r = 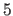 to ( to (
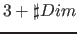 ), r = ), r = 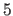 to ( to (
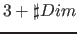 ) polarization fraction (as an angle in radians) in the dimension direction, which is spanned by the respective dimensions ) polarization fraction (as an angle in radians) in the dimension direction, which is spanned by the respective dimensions 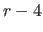 and and 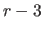 ( ( is the number of dimensions), the angular information is provided by the is the number of dimensions), the angular information is provided by the 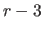 axis in positive direction, an electromagnetic wave is additive to other electromagnetic waves axis in positive direction, an electromagnetic wave is additive to other electromagnetic waves |
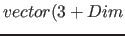 , , 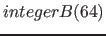 , ,
 , ,
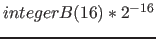 , ,
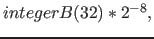
![$[integerB(16) * 2^{-16}]^{Dim-1} )$](img394.png) |
| property( periodBegin ) | Time in seconds (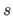 ) from the beginning of the whole multimedia object, from which the object is to be displayed; if possible, this property should be near the root of the multimedia object; when a multimedia object is played it can be determined with this property: the order in which subobjects should be evaluated and/or till which time to evaluate a part object ) from the beginning of the whole multimedia object, from which the object is to be displayed; if possible, this property should be near the root of the multimedia object; when a multimedia object is played it can be determined with this property: the order in which subobjects should be evaluated and/or till which time to evaluate a part object |
 , ,
 |
| property( periodEnd ) | Time in seconds (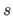 ) from the beginning of the whole multimedia object, till which the object is to be displayed; if possible, this property should be near the root of the multimedia object and follow a "periodBegin" property; when a multimedia object is played it can be determined with this property: the order in which subobjects should be evaluated and/or till which time to evaluate a part object completely ) from the beginning of the whole multimedia object, till which the object is to be displayed; if possible, this property should be near the root of the multimedia object and follow a "periodBegin" property; when a multimedia object is played it can be determined with this property: the order in which subobjects should be evaluated and/or till which time to evaluate a part object completely |
 , ,
 |
| property( evaluationTime ) | Time required for evaluating a multimedia object, in proportion to a multimedia object, which contains only one point (the value should be seen as a multiple of the evaluation time of a point); with this property in combination with the properties "periodBegin" und "periodEnd" a good evaluation order and time can be evalued for the partobjects, when playing a multimedia object; this property should stand immediately after (or below/within) the "periodBegin" and "periodEnd" properties |  , ,
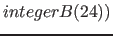 |
| property( checksum ) | A checksum for the object will be generated. The first parameter determines the type of the checksum. The second parameter specifies any which number of bits, a checksum is to be generated, and the third parameter defines how many bits the checksum is long. The last block of the checksum will be padded with 0 after loading the blocks, so that it too has the desired length. If there are enough bits to correct an existing error, it will be attempted to correct the error. (see section 21.3.3 on page ![[*]](../pictures/crossref.png) ) ) |
 , , 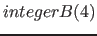 , , 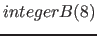 , , 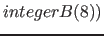 |
| property( boundSize ) | For the part object the border/size in bits will be stored, when saving it. If an error occured while loading the part object, the (in the bitstream after the faulty part object) following part objects can still be loaded, because their beginning is known. (see section 21.3.3 on page ![[*]](../pictures/crossref.png) ) ) |
 |




