Syntax:
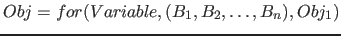





The area element defines a variable. It sets the defined variable to integers of a specified range of integers. The area element contains, in addition to the defined variables and the subobject to which it applies, a list of areas, which the variable will go through. The variable is valid everywhere in the subobject.
Syntax:
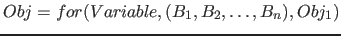
Description of the elements:
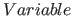 : The variable, which the area element defines.
: The variable, which the area element defines.
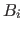
 are the areas. For the value
are the areas. For the value 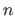 is
is 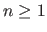 , so there is at least one subarea in the area element.
, so there is at least one subarea in the area element.
 : The subobject, for which the
: The subobject, for which the 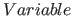 is defined and which will be evalued for every variable assignment of the area.
is defined and which will be evalued for every variable assignment of the area.
One (sub-)area 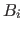 is a vector of degree 2, whose two integer components specify an integer field, to which the variable will be set. An area
is a vector of degree 2, whose two integer components specify an integer field, to which the variable will be set. An area 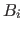 consists of the two (integers) elements of the vector
consists of the two (integers) elements of the vector 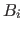 and all integers between them.
If one element of the vector is a variable, that contains a non-integer value, it is rounded to an integer. For the rounding, the decimal digit befor the point remains the same, if the first decimal digit after the point is between 0 to 4, otherwise (from 5 to 9) the number of the decimal befor the point is increased by one for positive numbers and decreases by one for negative numbers.
and all integers between them.
If one element of the vector is a variable, that contains a non-integer value, it is rounded to an integer. For the rounding, the decimal digit befor the point remains the same, if the first decimal digit after the point is between 0 to 4, otherwise (from 5 to 9) the number of the decimal befor the point is increased by one for positive numbers and decreases by one for negative numbers.
The area element includes as its area the union of all its subareas 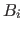 . It will therefore go through a range of all integers, which are contained in its subareas
. It will therefore go through a range of all integers, which are contained in its subareas 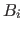 .
.
Examples:
![$for(x,[(1;3),(10;14)],Obj)$](img85.png) ; In this example, the variable
; In this example, the variable 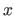 for the object
for the object  is set to the successive values: 1; 2; 3; 10; 11; 12; 13; 14
is set to the successive values: 1; 2; 3; 10; 11; 12; 13; 14
![$for(x,[(1;y=3.4985)],Obj)$](img86.png) ; In this example, the variable
; In this example, the variable 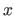 for the object
for the object  is set to the successive values: 1; 2; 3
is set to the successive values: 1; 2; 3
![$for(x,[(1;y=3.5)],Obj)$](img87.png) ; In this example, the variable
; In this example, the variable 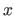 for the object
for the object  is set to the successive values: 1; 2; 3; 4
is set to the successive values: 1; 2; 3; 4
Note:
With this definition of the area element continuous functions can not be realized, because the area element just allows integers and dosn't allow continuous transition of values. Functions can only be realized continuous up to a certain point (e. g. in the range of integers).
Example:
The function 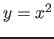 for the area
for the area
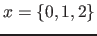 (chosen simple just for clarification)
(chosen simple just for clarification)
If it is tried to realize it in the form:
![$for(x,[(0;2)], fun(y,exp(x;2), p((x,y))))$](img90.png) gaps will result (in the transition from (1, 1) to (2, 4) a point (x, 3) is missing).
gaps will result (in the transition from (1, 1) to (2, 4) a point (x, 3) is missing).
However, this can be solved by "compression of the range":
![$for(x,[(0;6)], fun(sx, div(x,3), fun(y,exp(sx,2), p((sx,y)))))$](img91.png)
Now a point (2;3) exists (
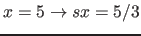 rounded up
rounded up  ;
;
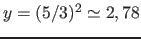 rounded up
rounded up 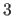 )
)
This has been choosen in favor for an easier implementation and better performance.
Multimedia objects (e. g. images) which are encoded in the Fib multimedia description language, will be made of individual dots (pixels) in the representation.
However, it is possible to achieve a scalability of a Fib multimedia object in other ways.




