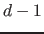 weggelassen. Der hier gegebene Algorithmus ist für mindestens drei Parameter (
weggelassen. Der hier gegebene Algorithmus ist für mindestens drei Parameter (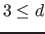 ). Wenn die Lösung nur zwei oder ein Parameter hat, kann ein anderer Algorithmus verwendet werden, bzw. der nachfolgende Algorthmus angepasst werden.
). Wenn die Lösung nur zwei oder ein Parameter hat, kann ein anderer Algorithmus verwendet werden, bzw. der nachfolgende Algorthmus angepasst werden.





Für die optimierte Lösung werden alle Randhyperebenen außer Punkten, Geraden und Hyperebenen der Dimensionalität 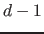 weggelassen. Der hier gegebene Algorithmus ist für mindestens drei Parameter (
weggelassen. Der hier gegebene Algorithmus ist für mindestens drei Parameter (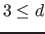 ). Wenn die Lösung nur zwei oder ein Parameter hat, kann ein anderer Algorithmus verwendet werden, bzw. der nachfolgende Algorthmus angepasst werden.
). Wenn die Lösung nur zwei oder ein Parameter hat, kann ein anderer Algorithmus verwendet werden, bzw. der nachfolgende Algorthmus angepasst werden.
 und
und  ) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von
) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von 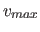 )
)
 :
:
 größer
größer 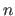 , setze
, setze  auf
auf 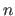 und gehe zu "8. Lösung ermitteln"
und gehe zu "8. Lösung ermitteln"
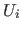
 für aktuelle Ungleichung
für aktuelle Ungleichung ![$U_i=U[i]$](img793.png) als Normalgleichung, mit dem Normalenvektor
als Normalgleichung, mit dem Normalenvektor 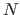 in Richtung der zulässigen Lösungen. Aus der Ungleichung
in Richtung der zulässigen Lösungen. Aus der Ungleichung 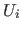 in der Form
in der Form
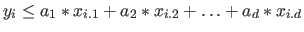 wird die Normalengleichung
wird die Normalengleichung
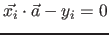 mit
mit
 und
und

 sie liegen
sie liegen
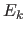 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 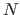 oder auf der Hyperebene -> erhöhe Zähler
oder auf der Hyperebene -> erhöhe Zähler  und gehe zu 1. (die Hyperfläche
und gehe zu 1. (die Hyperfläche  schränkt die Lösungsmenge nicht weiter ein, d. h.
schränkt die Lösungsmenge nicht weiter ein, d. h.  ist nicht relevant)
ist nicht relevant)
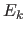 liegen nicht in Richtung des Normalenvektors
liegen nicht in Richtung des Normalenvektors 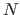 -> erniedrige Zähler
-> erniedrige Zähler  und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung
und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung 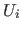 gäbe es keine Lösungen mehr, bzw. die Ungleichung
gäbe es keine Lösungen mehr, bzw. die Ungleichung 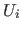 macht das bisherige Gleichungsystem unlösbar)
macht das bisherige Gleichungsystem unlösbar)
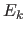 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 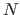 , andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche
, andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche  in den konvexer Hyperkörper der möglichen Lösungen
in den konvexer Hyperkörper der möglichen Lösungen
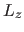 des Hyperkörpers
des Hyperkörpers  zwischen den Eckpunkten
zwischen den Eckpunkten 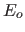 nicht in Richtung des Normalenvektors
nicht in Richtung des Normalenvektors 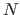 und Eckpunkten
und Eckpunkten 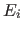 in dessen Richtung (ignoriere Eckpunkte
in dessen Richtung (ignoriere Eckpunkte 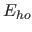 auf
auf  )
)
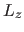 : ermittle Schnittpunkte
: ermittle Schnittpunkte 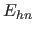 mit der Hyperfläche
mit der Hyperfläche  und füge sie zum Hyperkörper hinzu
und füge sie zum Hyperkörper hinzu
 , welche einen konvexen Körper bilden: für jeden Schnittpunkt
, welche einen konvexen Körper bilden: für jeden Schnittpunkt 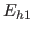 auf
auf  (
(
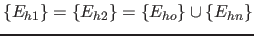 ) ermittle alle Schnittpunkt
) ermittle alle Schnittpunkt 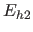 auf
auf  die gemeinsam auf mindestens
die gemeinsam auf mindestens 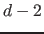 anderen Hyperflächen
anderen Hyperflächen 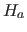 (
(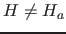 ) liegen. (Diese Hyperflächen sollten zusammen mit der Hyperfläche
) liegen. (Diese Hyperflächen sollten zusammen mit der Hyperfläche  als Schnittfläche eine Gerade haben. Da
als Schnittfläche eine Gerade haben. Da  die Dimensionalität
die Dimensionalität 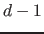 hat und der Schnitt mit jeder weiteren (
hat und der Schnitt mit jeder weiteren (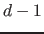 dimensionalen) Hyperflächen die Dimensionalität der Schnittfläche um eins verringert.)
dimensionalen) Hyperflächen die Dimensionalität der Schnittfläche um eins verringert.)
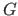 zwischen
zwischen 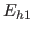 und
und 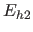 die gemeinsam auf gemeinsammen anderen Hyperfläche
die gemeinsam auf gemeinsammen anderen Hyperfläche 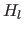 liegen
liegen
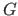 zu
zu  und als auf
und als auf  liegend hinzu
liegend hinzu
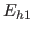 und
und 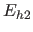 als auf
als auf 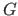 liegend hinzu
liegend hinzu
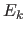 die nicht in Richtung des Normalenvektors
die nicht in Richtung des Normalenvektors 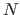 von
von  liegen
liegen
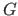 die nur noch einen Eckpunkt besitzen
die nur noch einen Eckpunkt besitzen
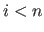 : erhöhe Zähler
: erhöhe Zähler  und gehe zu 1. (sonst 8.)
und gehe zu 1. (sonst 8.)
 als Eckpunkte der (konvexen) Lösungsmenge und
als Eckpunkte der (konvexen) Lösungsmenge und  als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich
als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich  ermittelt werden)
ermittelt werden)
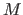 aller Eckpunkte
aller Eckpunkte 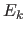 :
:
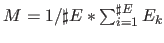
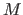 als Lösung und
als Lösung und  als Anzahl der erfüllten Ungleichungen zurück
als Anzahl der erfüllten Ungleichungen zurück




