




Next: Optimierte Lösung
Up: Lösung
Previous: Wichtige Daten:
Contents
Index
Das hier vorgestellte Verfahren ist optimiert. Alle überflüssigen Hyperebenen werden in ihm ignoriert.
- 0 Initialisiere die Hyperebenen (
 und
und  ) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von
) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von 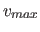 )
)
- 1 Prüfe
 :
:
- 1.1 Fall 1: Wenn
 größer
größer 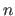 , setze
, setze  auf
auf 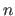 und gehe zu "8. Lösung ermitteln"
und gehe zu "8. Lösung ermitteln"
- 1.2 Sonst: Nehme nächste Ungleichung
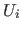
- 1.2.1 Erstelle eine orientierte Hyperfläche
 für aktuelle Ungleichung
für aktuelle Ungleichung ![$U_i=U[i]$](img793.png) als Normalgleichung, mit dem Normalenvektor
als Normalgleichung, mit dem Normalenvektor 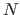 in Richtung der zulässigen Lösungen. Aus der Ungleichung
in Richtung der zulässigen Lösungen. Aus der Ungleichung 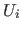 in der Form
in der Form
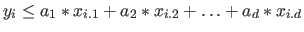 wird die Normalengleichung
wird die Normalengleichung
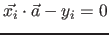 mit
mit
 und
und

- 2. Prüfe für alle Punkte auf welcher Seite der Hyperflache
 sie liegen
sie liegen
- 2.1 Fall 1: alle Eckpunkte
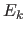 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 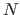 oder auf der Hyperebene -> erhöhe Zähler
oder auf der Hyperebene -> erhöhe Zähler  und gehe zu 1. (die Hyperfläche
und gehe zu 1. (die Hyperfläche  schränkt die Lösungsmenge nicht weiter ein, d. h.
schränkt die Lösungsmenge nicht weiter ein, d. h.  ist nicht relevant)
ist nicht relevant)
- 2.2 Fall 2: alle Eckpunkte
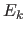 liegen nicht in Richtung des Normalenvektors
liegen nicht in Richtung des Normalenvektors 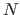 -> erniedrige Zähler
-> erniedrige Zähler  und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung
und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung 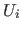 gäbe es keine Lösungen mehr, bzw. die Ungleichung
gäbe es keine Lösungen mehr, bzw. die Ungleichung 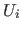 macht das bisherige Gleichungsystem unlösbar)
macht das bisherige Gleichungsystem unlösbar)
- 2.3 Sonst: einige Eckpunkte
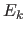 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 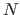 , andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche
, andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche  in den konvexer Hyperkörper der möglichen Lösungen
in den konvexer Hyperkörper der möglichen Lösungen
- 3. Für jede Hyperfläche
 mit der Dimensionalität
mit der Dimensionalität 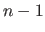 (diese entsprechen den Ungleichungen) aus
(diese entsprechen den Ungleichungen) aus  (konvexer Hyperkörper der möglichen Lösungen):
(konvexer Hyperkörper der möglichen Lösungen):
- 3.1 Berechne die Schnittebene (Dimensionalität ist
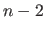 ) von
) von  und
und 
- 3.1.1 Fall 1: wenn keine Schnittebene existiert -> gehe zu 3.1 und prüfe die nächste Hyperfläche

- 3.1.2 Sonst: wenn eine Schnittebene
 existiert:
existiert:
- 3.1.2.1 Wenn eine identische Hyperfläche wie die Schnittebene
 in den Hyperflächen
in den Hyperflächen  existiert (bzw. es existiert keine neue Hyperfläche)
existiert (bzw. es existiert keine neue Hyperfläche)
- 3.1.2.1.1 Vermerke zu der gefundenen Schnittebene als Verweise die Hyperfläche
 als die enthaltende Hyperfläche
als die enthaltende Hyperfläche
- 3.1.2.1.2 Füge zu der Hyperfläche
 als Verweise die Schnittebene
als Verweise die Schnittebene  als eine enthaltende Hyperflächen hinzu
als eine enthaltende Hyperflächen hinzu
- 3.1.2.1.3 gehe zu 3.1 und prüfe die nächste Hyperfläche

- 3.1.2.2 Vermerke zu der Schnittebene
 als Verweise die Hyperflächen
als Verweise die Hyperflächen  und
und  als die enthaltenden Hyperflächen
als die enthaltenden Hyperflächen
- 3.1.2.3 Füge zu den Hyperflächen
 und
und  als Verweise die Schnittebene
als Verweise die Schnittebene  als eine enthaltende Hyperflächen hinzu
als eine enthaltende Hyperflächen hinzu
- 3.1.2.4 Füge Schnittebene
 zu der Liste
zu der Liste 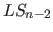 mit noch zu prüfenden Schnittebene hinzu
mit noch zu prüfenden Schnittebene hinzu
- 3.1.2.5 Füge die Schnittebene
 zu den Hyperflächen
zu den Hyperflächen  hinzu
hinzu
- 3.1.2.6 Gehe zu 3.1 und prüfe die nächste Hyperfläche

- 4. Füge Schnittebenen der Schnittebenen hinzu: für
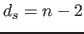 bis
bis 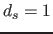 (
(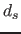 ist die Dimensionalität der geprüften Schnittebenen)
ist die Dimensionalität der geprüften Schnittebenen)
- 4.1 Nehme und entferne die letzte Schnittebene
 von der List
von der List 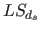 (mit den noch zu prüfenden Schnittebene der Dimensionalität
(mit den noch zu prüfenden Schnittebene der Dimensionalität 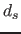 ):
):
- 4.1.1 Für jede Hyperfläche
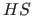 die
die  enthält:
enthält:
- 4.1.1.1 Für jede Hyperfläche
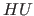 die in
die in 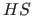 enthalten ist (
enthalten ist (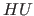 hat Dimensionalität
hat Dimensionalität 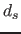 )
)
- 4.1.1.1.1 Berechne Schnittebene
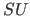 (hat Dimensionalität
(hat Dimensionalität 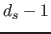 ) von
) von  und
und 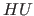
- 4.1.1.1.1 Fall 1: wenn keine Schnittebene
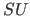 existiert -> gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche
existiert -> gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche 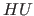
- 4.1.1.1.1 Sonst: wenn eine Schnittebene
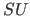 existiert:
existiert:
- 4.1.1.1.1.1 Wenn eine identische Hyperfläche (diese sollte in
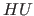 schon enthalten sein) wie die Schnittebene
schon enthalten sein) wie die Schnittebene 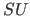 in den Hyperflächen
in den Hyperflächen  existiert (bzw. es existiert keine neue Schnitthyperfläche)
existiert (bzw. es existiert keine neue Schnitthyperfläche)
- 4.1.1.1.1.1.1 Vermerke zu der gefundenen Schnittebene als Verweise die Hyperfläche
 als die enthaltende Hyperfläche
als die enthaltende Hyperfläche
- 4.1.1.1.1.1.2 Füge zu der Hyperfläche
 als Verweis die Schnittebene
als Verweis die Schnittebene 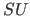 für eine enthaltende Hyperflächen hinzu
für eine enthaltende Hyperflächen hinzu
- 4.1.1.1.1.1.3 gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche
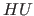
- 4.1.1.1.1.2 Vermerke zu der Schnittebene
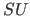 als Verweise die Hyperflächen
als Verweise die Hyperflächen  und
und 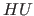 als die enthaltenden Hyperflächen
als die enthaltenden Hyperflächen
- 4.1.1.1.1.3 Füge zu den Hyperflächen
 und
und 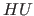 als Verweise die Schnittebene
als Verweise die Schnittebene 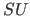 für eine enthaltende Hyperflächen hinzu
für eine enthaltende Hyperflächen hinzu
- 4.1.1.1.1.4 Füge Schnittebene
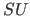 zu der Liste
zu der Liste 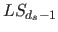 mit noch zu prüfenden Schnittebene hinzu
mit noch zu prüfenden Schnittebene hinzu
- 4.1.1.1.1.5 Füge die Schnittebene
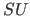 zu den Hyperflächen
zu den Hyperflächen  hinzu
hinzu
- 4.1.1.1.1.6 Gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche
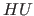
- 4.2 Wenn
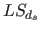 nicht leer ist, gehe zu 4.1
nicht leer ist, gehe zu 4.1
- 4.3 Wenn
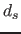 größer
größer 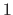 ist ernidrige
ist ernidrige 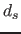 und gehe zu 4
und gehe zu 4
- 5. Entferne alle nicht mehr benötigten Eckpunkte:
- 5.1 Entferne alle Eckpunkte (bzw. Hyperflächen der Dimensionalität 0), inclusive Verweise auf sie, aus
 und
und  die nicht in Richtung des Normalenvektors
die nicht in Richtung des Normalenvektors 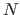 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  liegen (bzw. entferne die Eckpunkte, welche die Hyperfläche
liegen (bzw. entferne die Eckpunkte, welche die Hyperfläche  aus dem Hyperkörper der möglichen Lösungen
aus dem Hyperkörper der möglichen Lösungen  abschneidet)
abschneidet)
- 5.2 Entferne die Überflüssigen Eckpunkte die durch
 hinzukamen, nehme und entferne den letzten Eckpunkte
hinzukamen, nehme und entferne den letzten Eckpunkte  von der List
von der List 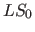 mit noch zu prüfenden Schnittebene der Dimensionalität
mit noch zu prüfenden Schnittebene der Dimensionalität 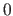 :
:
- 5.2.1 Für jede Hyperfläche bzw. Gerade
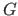 die
die  enthält:
enthält:
- 5.2.1.1 Fall 1: Enthält die Gerade
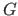 maximal zwei Eckpunkte bzw. Hyperebenen -> gehe zu 5.2.1 und prüfe die nächste Gerade
maximal zwei Eckpunkte bzw. Hyperebenen -> gehe zu 5.2.1 und prüfe die nächste Gerade 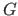
- 5.2.1.2 Sonst: Enthält die Gerade
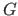 mehr als zwei (bzw. drei) Eckpunkte bzw. Hyperebenen (die Eckpunkte bilden dann keinen konvexen Körper auf
mehr als zwei (bzw. drei) Eckpunkte bzw. Hyperebenen (die Eckpunkte bilden dann keinen konvexen Körper auf 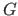 mehr):
mehr):
- 5.2.1.2.1 Ermittle den mittleren Punkt
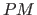 der drei Schnittpunkte auf
der drei Schnittpunkte auf 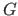 (bzw. enthaltenden Hyperebenen) und die beiden anderen Punkte
(bzw. enthaltenden Hyperebenen) und die beiden anderen Punkte 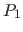 und
und 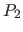
- 5.2.1.2.2 Für jede Hyperfläche
 mit der Dimensionalität
mit der Dimensionalität 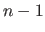 (diese entsprechen den begrenzenden Ungleichungen
(diese entsprechen den begrenzenden Ungleichungen 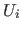 ) aus
) aus  die den Punkt
die den Punkt 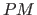 (indirekt) enthält:
(indirekt) enthält:
- 5.2.1.2.2.1 Fall 1: beide Punkt
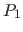 und
und 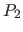 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 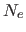 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  oder auf
oder auf  (also in der Lösungsmenge) -> gehe zu 5.2.1.2.2 und prüfe die nächste Hyperfläche
(also in der Lösungsmenge) -> gehe zu 5.2.1.2.2 und prüfe die nächste Hyperfläche 
- 5.2.1.2.2.2 Sonst: der Punkt
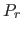 liegen nicht in Richtung des Normalenvektors
liegen nicht in Richtung des Normalenvektors 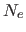 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  oder auf
oder auf  (also ist er nicht in der Lösungsmenge)
(also ist er nicht in der Lösungsmenge)
- 5.2.1.2.2.2.1 Entferne den Punkt
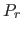 aus der Menge der Eckpunkte
aus der Menge der Eckpunkte  (inclusive Verweise auf ihn)
(inclusive Verweise auf ihn)
- 5.2.1.2.2.2.1 Wenn
 nicht entfernt wurde (
nicht entfernt wurde (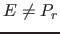 ), gehe zu Schritt 5.2.1 und prüfe die nächste Gerade
), gehe zu Schritt 5.2.1 und prüfe die nächste Gerade 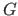 , sonst gehe zu 5.2 und prüfe den nächsten Eckpunkt
, sonst gehe zu 5.2 und prüfe den nächsten Eckpunkt 
- 6. Entferne alle nicht mehr benötigten Hyperflächen: für
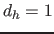 bis
bis 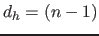 (Dies sind alle Hyperflächen, die keine Eckpunkte des konvexen Hyperkörper der Lösungen enthalten und damit nicht zu ihm gehören.)
(Dies sind alle Hyperflächen, die keine Eckpunkte des konvexen Hyperkörper der Lösungen enthalten und damit nicht zu ihm gehören.)
- 6.1 Entferne alle Hyperflachen, inclusive Verweise zu ihnen, der Dimensionalität
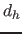 die keine Hyperflächen (diese haben Dimensionalität
die keine Hyperflächen (diese haben Dimensionalität 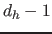 ) mehr enthalten
) mehr enthalten
- 7. wenn
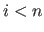 : erhöhe Zähler
: erhöhe Zähler  und gehe zu 1. (sonst 8.)
und gehe zu 1. (sonst 8.)
- 8. Lösung ermitteln:
- 8.1. Alternative 1:
- 8.1.1. Gebe
 als Eckpunkte der (konvexen) Lösungsmenge und
als Eckpunkte der (konvexen) Lösungsmenge und  als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich
als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich  ermittelt werden)
ermittelt werden)
- 8.1. Alternative 2:
- 8.1.1. Nehme den Mittelpunkt /Schwerpunkt
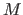 aller Eckpunkte
aller Eckpunkte 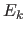 :
:
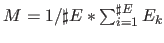
- 8.1.2. Gebe
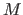 als Lösung und
als Lösung und  als Anzahl der erfüllten Ungleichungen zurück
als Anzahl der erfüllten Ungleichungen zurück





Next: Optimierte Lösung
Up: Lösung
Previous: Wichtige Daten:
Contents
Index
Betti Österholz
2013-02-13
 und
und  ) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von
) mit dem Hyperkörper der maximalen Lösungsmenge (eventuell unter Zuhilfenahme von 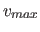 )
)
 :
:
 größer
größer 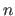 , setze
, setze  auf
auf 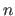 und gehe zu "8. Lösung ermitteln"
und gehe zu "8. Lösung ermitteln"
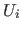
 für aktuelle Ungleichung
für aktuelle Ungleichung ![$U_i=U[i]$](img793.png) als Normalgleichung, mit dem Normalenvektor
als Normalgleichung, mit dem Normalenvektor 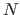 in Richtung der zulässigen Lösungen. Aus der Ungleichung
in Richtung der zulässigen Lösungen. Aus der Ungleichung 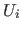 in der Form
in der Form
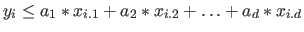 wird die Normalengleichung
wird die Normalengleichung
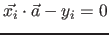 mit
mit
 und
und

 sie liegen
sie liegen
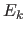 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 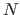 oder auf der Hyperebene -> erhöhe Zähler
oder auf der Hyperebene -> erhöhe Zähler  und gehe zu 1. (die Hyperfläche
und gehe zu 1. (die Hyperfläche  schränkt die Lösungsmenge nicht weiter ein, d. h.
schränkt die Lösungsmenge nicht weiter ein, d. h.  ist nicht relevant)
ist nicht relevant)
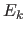 liegen nicht in Richtung des Normalenvektors
liegen nicht in Richtung des Normalenvektors 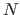 -> erniedrige Zähler
-> erniedrige Zähler  und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung
und gehe zu "8. Lösung ermitteln" (durch die Hinzunahme der Ungleichung 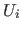 gäbe es keine Lösungen mehr, bzw. die Ungleichung
gäbe es keine Lösungen mehr, bzw. die Ungleichung 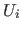 macht das bisherige Gleichungsystem unlösbar)
macht das bisherige Gleichungsystem unlösbar)
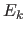 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 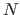 , andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche
, andere nicht -> gehe zu Schritt 3., bzw. integriere die Hyperfläche  in den konvexer Hyperkörper der möglichen Lösungen
in den konvexer Hyperkörper der möglichen Lösungen
 mit der Dimensionalität
mit der Dimensionalität 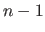 (diese entsprechen den Ungleichungen) aus
(diese entsprechen den Ungleichungen) aus  (konvexer Hyperkörper der möglichen Lösungen):
(konvexer Hyperkörper der möglichen Lösungen):
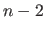 ) von
) von  und
und 

 existiert:
existiert:
 in den Hyperflächen
in den Hyperflächen  existiert (bzw. es existiert keine neue Hyperfläche)
existiert (bzw. es existiert keine neue Hyperfläche)
 als die enthaltende Hyperfläche
als die enthaltende Hyperfläche
 als Verweise die Schnittebene
als Verweise die Schnittebene  als eine enthaltende Hyperflächen hinzu
als eine enthaltende Hyperflächen hinzu

 als Verweise die Hyperflächen
als Verweise die Hyperflächen  und
und  als die enthaltenden Hyperflächen
als die enthaltenden Hyperflächen
 und
und  als Verweise die Schnittebene
als Verweise die Schnittebene  als eine enthaltende Hyperflächen hinzu
als eine enthaltende Hyperflächen hinzu
 zu der Liste
zu der Liste 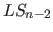 mit noch zu prüfenden Schnittebene hinzu
mit noch zu prüfenden Schnittebene hinzu
 zu den Hyperflächen
zu den Hyperflächen  hinzu
hinzu

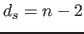 bis
bis 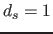 (
(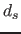 ist die Dimensionalität der geprüften Schnittebenen)
ist die Dimensionalität der geprüften Schnittebenen)
 von der List
von der List 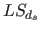 (mit den noch zu prüfenden Schnittebene der Dimensionalität
(mit den noch zu prüfenden Schnittebene der Dimensionalität 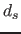 ):
):
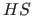 die
die  enthält:
enthält:
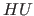 die in
die in 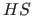 enthalten ist (
enthalten ist (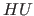 hat Dimensionalität
hat Dimensionalität 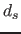 )
)
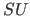 (hat Dimensionalität
(hat Dimensionalität 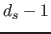 ) von
) von  und
und 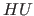
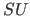 existiert -> gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche
existiert -> gehe zu 4.1.1.1 und prüfe die nächste Hyperfläche 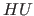
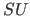 existiert:
existiert:
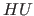 schon enthalten sein) wie die Schnittebene
schon enthalten sein) wie die Schnittebene 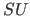 in den Hyperflächen
in den Hyperflächen  existiert (bzw. es existiert keine neue Schnitthyperfläche)
existiert (bzw. es existiert keine neue Schnitthyperfläche)
 als die enthaltende Hyperfläche
als die enthaltende Hyperfläche
 als Verweis die Schnittebene
als Verweis die Schnittebene 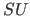 für eine enthaltende Hyperflächen hinzu
für eine enthaltende Hyperflächen hinzu
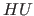
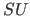 als Verweise die Hyperflächen
als Verweise die Hyperflächen  und
und 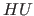 als die enthaltenden Hyperflächen
als die enthaltenden Hyperflächen
 und
und 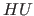 als Verweise die Schnittebene
als Verweise die Schnittebene 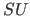 für eine enthaltende Hyperflächen hinzu
für eine enthaltende Hyperflächen hinzu
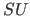 zu der Liste
zu der Liste 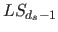 mit noch zu prüfenden Schnittebene hinzu
mit noch zu prüfenden Schnittebene hinzu
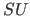 zu den Hyperflächen
zu den Hyperflächen  hinzu
hinzu
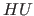
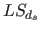 nicht leer ist, gehe zu 4.1
nicht leer ist, gehe zu 4.1
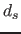 größer
größer 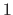 ist ernidrige
ist ernidrige 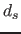 und gehe zu 4
und gehe zu 4
 und
und  die nicht in Richtung des Normalenvektors
die nicht in Richtung des Normalenvektors 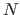 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  liegen (bzw. entferne die Eckpunkte, welche die Hyperfläche
liegen (bzw. entferne die Eckpunkte, welche die Hyperfläche  aus dem Hyperkörper der möglichen Lösungen
aus dem Hyperkörper der möglichen Lösungen  abschneidet)
abschneidet)
 hinzukamen, nehme und entferne den letzten Eckpunkte
hinzukamen, nehme und entferne den letzten Eckpunkte  von der List
von der List 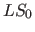 mit noch zu prüfenden Schnittebene der Dimensionalität
mit noch zu prüfenden Schnittebene der Dimensionalität 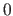 :
:
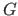 die
die  enthält:
enthält:
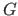 maximal zwei Eckpunkte bzw. Hyperebenen -> gehe zu 5.2.1 und prüfe die nächste Gerade
maximal zwei Eckpunkte bzw. Hyperebenen -> gehe zu 5.2.1 und prüfe die nächste Gerade 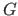
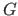 mehr als zwei (bzw. drei) Eckpunkte bzw. Hyperebenen (die Eckpunkte bilden dann keinen konvexen Körper auf
mehr als zwei (bzw. drei) Eckpunkte bzw. Hyperebenen (die Eckpunkte bilden dann keinen konvexen Körper auf 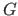 mehr):
mehr):
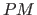 der drei Schnittpunkte auf
der drei Schnittpunkte auf 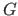 (bzw. enthaltenden Hyperebenen) und die beiden anderen Punkte
(bzw. enthaltenden Hyperebenen) und die beiden anderen Punkte 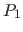 und
und 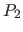
 mit der Dimensionalität
mit der Dimensionalität 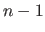 (diese entsprechen den begrenzenden Ungleichungen
(diese entsprechen den begrenzenden Ungleichungen 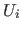 ) aus
) aus  die den Punkt
die den Punkt 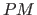 (indirekt) enthält:
(indirekt) enthält:
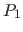 und
und 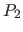 liegen in Richtung des Normalenvektors
liegen in Richtung des Normalenvektors 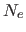 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  oder auf
oder auf  (also in der Lösungsmenge) -> gehe zu 5.2.1.2.2 und prüfe die nächste Hyperfläche
(also in der Lösungsmenge) -> gehe zu 5.2.1.2.2 und prüfe die nächste Hyperfläche 
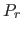 liegen nicht in Richtung des Normalenvektors
liegen nicht in Richtung des Normalenvektors 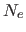 der Hyperfläche
der Hyperfläche  von einer Seite von
von einer Seite von  oder auf
oder auf  (also ist er nicht in der Lösungsmenge)
(also ist er nicht in der Lösungsmenge)
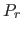 aus der Menge der Eckpunkte
aus der Menge der Eckpunkte  (inclusive Verweise auf ihn)
(inclusive Verweise auf ihn)
 nicht entfernt wurde (
nicht entfernt wurde (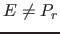 ), gehe zu Schritt 5.2.1 und prüfe die nächste Gerade
), gehe zu Schritt 5.2.1 und prüfe die nächste Gerade 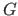 , sonst gehe zu 5.2 und prüfe den nächsten Eckpunkt
, sonst gehe zu 5.2 und prüfe den nächsten Eckpunkt 
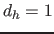 bis
bis 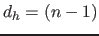 (Dies sind alle Hyperflächen, die keine Eckpunkte des konvexen Hyperkörper der Lösungen enthalten und damit nicht zu ihm gehören.)
(Dies sind alle Hyperflächen, die keine Eckpunkte des konvexen Hyperkörper der Lösungen enthalten und damit nicht zu ihm gehören.)
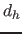 die keine Hyperflächen (diese haben Dimensionalität
die keine Hyperflächen (diese haben Dimensionalität 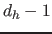 ) mehr enthalten
) mehr enthalten
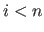 : erhöhe Zähler
: erhöhe Zähler  und gehe zu 1. (sonst 8.)
und gehe zu 1. (sonst 8.)
 als Eckpunkte der (konvexen) Lösungsmenge und
als Eckpunkte der (konvexen) Lösungsmenge und  als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich
als Anzahl der erfüllten Ungleichungen zurück (eine Lösung kann dann aus dem Bereich  ermittelt werden)
ermittelt werden)
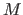 aller Eckpunkte
aller Eckpunkte 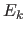 :
:
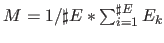
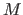 als Lösung und
als Lösung und  als Anzahl der erfüllten Ungleichungen zurück
als Anzahl der erfüllten Ungleichungen zurück




