




Next: The genetic algorithm
Up: Theoretical statements for the
Previous: Cardinality of Fib
Contents
Index
Any complete Fib object can be represented as a multimedia object
It is shown in this section, that it is always possible to interpret (to translate into a multimedia object) any complete Fib object (see section 11.2 on page ![[*]](../pictures/crossref.png) ) in a way, that only valid multimedia objects of a certain type (e. g. RGB images with 100 x 100 pixels) can result. In which the limitations with regard to the multimedia data, as already mentioned, are assumed, that the multimedia data can be represented as properties of points of a finite, euclidean and discrete (there are smallest units) space. This restriction is not very large, because they (almost) excludes non of the presently common multimedia data. The multimedia data may therefore represent images, sound or movies.
) in a way, that only valid multimedia objects of a certain type (e. g. RGB images with 100 x 100 pixels) can result. In which the limitations with regard to the multimedia data, as already mentioned, are assumed, that the multimedia data can be represented as properties of points of a finite, euclidean and discrete (there are smallest units) space. This restriction is not very large, because they (almost) excludes non of the presently common multimedia data. The multimedia data may therefore represent images, sound or movies.
With the restriction that the distance / difference between two properties of the same type can always be determined as a numerical value, two multimedia objects with the same dimensions can be always compared. Two multimedia objects have the same dimensions, if for each point in the first multimedia object exactly one corresponding point in the other multimedia object exists.
The requirement of the complete Fib object is necessary to ensure that the Fib object can be always evaluated. Since the completeness of an Fib object can be check with the syntax shown in part II, if a Fib object is complete can always be determined. Incomplete Fib objects should not be generated by the algorithms or the genetic operators.
If the dimensions of a Fib object are adapted to that of a multimedia object (this should be always possible), the Fib object is always comparable with the multimedia object, because it can itself be always presented as a multimedia object, and two multimedia objects with the same dimensions can always be compared to each other and the similarity to each other can be evaluated.
Note: This is advantageous for genetic algorithms. In some other forms of representation that are generated by genetic algorithms, invalid objects (e. g. programs) arise, where a more accurate evaluation / comparison is not possible. A population in this format can contain, for example, a large class of objects that are invalid, which are all equally bad and are therefore considered same in the selection process. If the population consists only of invalid individuals, the selection of a better individual is impossible. The genetic algorithm is then on a (fitness) plane, from which it can only find away with great difficulty.
Proof that every correct Fib object can be represented as a multimedia object (of a specific type, such as a picture):
The starting point is that a multimedia object (euclidean, two-dimensional, discrete) can be represented as a finite set of points with their (finitely many) properties. Since there are only finitely many points with only finitely many properties, such a finite set is always constructible.
Such a finite set of points with their (finitely many) properties is also generated by a correct Fib object. Points of the set that are too much to represent a multimedia object, will be deleted from the set. Points that are missing in the set to represent a multimedia object are inserted into the set. Properties of the points that are too much to represent a multimedia object will be deleted. Properties, which are missing at points to represent a multimedia object, are added and set with their default values (e. g. the zero values of their domains). In this way a finite set of points is created with their (finite many) properties that can be represented as a multimedia object.
Example: The Fib object should represent an RGB image with 100 x 100 pixels. For this the dimensions of the Fib object are adjusted to cover these 100 x 100 pixels in horizontal and vertical direction. That is, if the dimension (horizontal or vertical) already exists, the domain of each direction is adjusted, so that it covers at least 100 values at regular intervals. So that to each pixel a value is assigned. If a dimension (/ direction) is missing, it will be created with the appropriate domain and in all points for the dimension the standard value of 0 will be set. In this case there is no point with other values than the default value for this dimension. Dimensions that are too much, are deleted from the root elements and the points. The evaluation of the resulting Fib object produces a set of points with their properties. During evaluation, the smallest value of 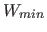 of each dimension in the Fib object is assigned to the value 0 as the coordinate in the set, the second smallest one to 1 as the coordinate, etc.
of each dimension in the Fib object is assigned to the value 0 as the coordinate in the set, the second smallest one to 1 as the coordinate, etc.
From this set now all points are deleted that are not within the 100 x 100 pixels boundary (points for which a coordinate respectively value is less than 0 or greater than 99). For all coordinates, which are still missing (missing points, where the values respectively the coordinates is between [including] 0 and 99), points are inserted. All properties that are not RGB colors will be deleted. To all points that have no property for RGB colors, the default color
 is assigned. The resulting set contains for each point in the RGB image with 100 x 100 pixels a point with RGB color, but no other points or properties, and thus represents an RGB image with 100 x 100 pixels.
is assigned. The resulting set contains for each point in the RGB image with 100 x 100 pixels a point with RGB color, but no other points or properties, and thus represents an RGB image with 100 x 100 pixels.
This can then be compared with other RGB images with 100 x 100 pixels and rated in relation to them.





Next: The genetic algorithm
Up: Theoretical statements for the
Previous: Cardinality of Fib
Contents
Index
Betti Österholz
2013-02-13
![[*]](../pictures/crossref.png) ) in a way, that only valid multimedia objects of a certain type (e. g. RGB images with 100 x 100 pixels) can result. In which the limitations with regard to the multimedia data, as already mentioned, are assumed, that the multimedia data can be represented as properties of points of a finite, euclidean and discrete (there are smallest units) space. This restriction is not very large, because they (almost) excludes non of the presently common multimedia data. The multimedia data may therefore represent images, sound or movies.
) in a way, that only valid multimedia objects of a certain type (e. g. RGB images with 100 x 100 pixels) can result. In which the limitations with regard to the multimedia data, as already mentioned, are assumed, that the multimedia data can be represented as properties of points of a finite, euclidean and discrete (there are smallest units) space. This restriction is not very large, because they (almost) excludes non of the presently common multimedia data. The multimedia data may therefore represent images, sound or movies.





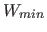 of each dimension in the Fib object is assigned to the value 0 as the coordinate in the set, the second smallest one to 1 as the coordinate, etc.
of each dimension in the Fib object is assigned to the value 0 as the coordinate in the set, the second smallest one to 1 as the coordinate, etc.
 is assigned. The resulting set contains for each point in the RGB image with 100 x 100 pixels a point with RGB color, but no other points or properties, and thus represents an RGB image with 100 x 100 pixels.
is assigned. The resulting set contains for each point in the RGB image with 100 x 100 pixels a point with RGB color, but no other points or properties, and thus represents an RGB image with 100 x 100 pixels.