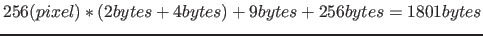Power of the Fib multimedia language on images

With the Fib multimedia language all as raster graphics displayable images can be represented. Images, that are displayed as raster graphics, are the most commonly used images in the digital data processing. These include Windows bitmap (BMP; file extension: .bmp), JPEG File Interchange Format (JFIF, file extension: .jpg) and Portable Network Graphics (PNG, File Extension: .png).

With using only the point element and the list element alone all possible raster graphics can (already) be represented.

Proof: A raster graphic (euclidean, two dimensional, discrete) can be represented as a matrix, the column indicats the x coordinate, the lines the y coordinate of the point and the values specify the colors of the points. The number of dots in the raster image is finite. To represent these points in the Fib multimedia language, a root-element have to be created that contains the properties of the raster graphic (size and dimension domain etc.). In this root-element a main Fib object, wich is a list element, is inserted, which contains for each point of the image a subobject. This subobject consists only of a property element, which encodes the color of the point, and one contained point element, which encodes the position of the point. So there is for every point in the raster graphic a corresponding point in the generated Fib object, so that the Fib object represents the raster image.

A mapping into the Fib multimedia language can for example be implemented by the algorithm shown in listing 2 (pseudo-C).

The indexing of the matrix begins with (0.0).

The color value of coordinates (x, y) can be determined with matrix[ x, y ]. With the function getColorVector() a Fib color vector is generated from the matrix color value.

The syntax of the Fib objects corresponds to the in section II on page discussed possible syntax.

Since the expansion with functions and other elements is optional, a correct Fib object is generated with the specified algorithm.

For each point in the matrix there is a same-colored point in the Fib object with the corresponding coordinate, but there are no points in Fib object that are not present in the matrix, because each coordinate of the matrix is traverse with the two "for" loops. Thereby a point in the Fib object is added for each coordinate and thus for every point in the raster graphic. Thus for every point in the raster graphic a corresponding point in the Fib object exists. Since only coordinates of the matrix are traverse in the "for" loops and only for them corresponding points are included in the Fib object, there are only points that appear in the matrix and hence only points in the Fib object, which also occur in the raster graphic. So there are only the points from the original raster graphic in the Fib object and no more. Thus the Fib object and the original the raster graphic represent (/shows) the same raster graphic. Therefore, all raster graphics are representable with the Fib multimedia language.

A Fib object generated by the algorithm, that represents an original raster graphic, is an upper limit to the minimum size of possible corresponding Fib objects. This means, each raster graphic can be represented by a Fib object, that is as big as the Fib object for the raster graphics that was generated with the above algorithm, that is the Fib object generated. But there are likely even shorter Fib objects for raster graphics.

With that the minimum size of a Fib object for a raster graphic is maximal:

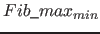$Fib\_max_{min}$ = (number of pixels in the image) 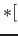$* [$(size of a point element) + (size of a property element for the appropriate color scheme)$]$ + (size of a list element)+ (size of a root-element with values set)

Example: You want to shown an image of 8 x 8 = 256 pixels with 3 bytes for the color (RGB), 1 byte for the position (for each direction x and y 4 bits = 8 possible values) and 1 byte for the object name (for example "l" for the list elements and "p" for the point elements). Parentheses are not needed, because all parts have a fixed length. (The assumptions about the sizes of the Fib object elements are estimated here. In a implementation, better (/smaller) values are more likely.)

• A point element requires 2 bytes (1 byte position + 1 byte element name).
• For a property element 4 bytes are needed (3 bytes color + 1 byte element name).
• For a list element 9 bytes are needed (8 bytes for specifying the number of subobjects + 1 byte element name).
• The root-element requires 256 bytes. (Since many parts of the root-element are empty and only the domain for two dimensions and the RGB color domain must be specified, 256 bytes should be enough.)

Calculation: $256 (pixel) * (2 bytes + 4 bytes) + 9 bytes + 256 bytes = 1801 bytes$

So the image can definitely be displayed with a 1801 byte long Fib object. But there are other shorter Fib object representations possible. The 1801 bytes are thus the upper limit for the minimum size with which the image can be represented by a Fib object.

For comparison: The memory requirements of a raster image as a bitmap (only point information) is at least (Number of pixels in the image) * (size of a color value)

For the above example it results in: $256 (pixel) * 3 bytes = 768 bytes$

That's about half of the 1801 byte limit on the minimum Fib object representation.

In that the matrix is extended to three dimensions, the statement about the representability of all raster images can be easily extended to sequences of raster images (such as the images of movies).